Why you need to get the line right when swimming across the current
In our previous newsletter we looked at the how swimming with or against the current affects your speed. This time we look at swimming across a current. It’s worth thinking about this as it can make a huge difference to your time if you get things wrong.
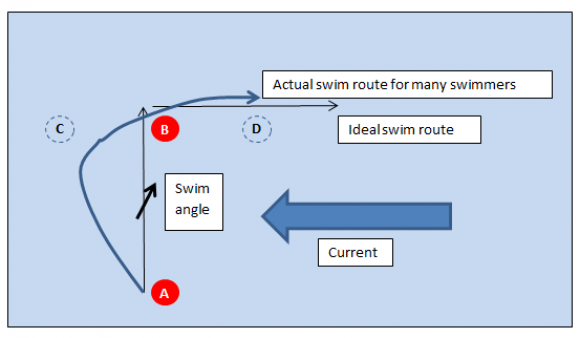
One of our National Series races this summer was held in the sea at Bournemouth. The course was a rectangle, firstly heading directly out to sea, then turning right for a long stretch parallel to the shore, turning right again for a short stretch back towards the coast and then a final long stretch again parallel to the beach. As well as a good deal of chop and swell that day swimmers also had to deal with a strong current moving from right to left along the coast. This caused many participants to swim a lot further than necessary as shown on the sketch below.
The diagram above shows what happened to swimmers who weren’t aware of or didn’t compensate for the current. Instead of taking the shortest route from buoy A to buoy B they allowed the current to drag them towards point C. When they realised they had to swim against the current to correct their course.
In the worst case, if a swimmer aimed towards B and swam perpendicular to the shore they would end up at point C. To see how damaging to your race prospects this might be, let’s put in some numbers.
- Swimmer speed = 1 m/s (equivalent to 100m in 1:40.0)
- Current speed = 0.3 m/s (we’ve no idea what it really was, this is just to illustrate the problem)
- Distance AB = 200m (just a number to do sums with)
If this swimmer headed out directly from the shore and swam for 200 seconds they would end up at point C. Point C is 200 x 0.3 = 60m to the left of the turning buoy B. The swimmer would then have to swim 60m against the current, which would take 60/(1-0.3) = 85.7 seconds.
Total time to reach point B = 285.7 seconds.
A second swimmer also swims at 1m/s but angles his (or her) body towards point D from the beginning, and maintains this angle until reaching point B. The direction of travel is A to B even though the swimmer is aiming towards D because the angle of swim counteracts the current. The effective distance swum is AD, which is the same as AC and hence equals the square route of (AB^2 + BC^2) = 208.8m. (i.e. using Pythagoras’s theorem)
Thus time to reach point B = 208.8 seconds
The second swimmer will therefore reach buoy B 76.9 seconds in front of the first swimmer.
To achieve this the swimmer will need to angle his body at 16.7 degrees to the direction of travel (see the swim angle arrow). (tan-1(BD/AB))
Of course, in a real swim you probably won’t know the variables nor will you be inclined to carry out such calculations. Picking the right line becomes a question of experience and judgement but bear this in mind next time you’re swimming across a current and you could find yourself jumping far ahead of your competitors.